3. circlespacking module¶

Module to define particular circular tangents in a closed polygon in \(\mathbb{R}^2\).

class circlespacking.pckCirclesInPolygon(coordinates, depth=None)[source]¶

Bases: object

Creates an instance of an object that defines circular particles tangent in a fractal way inside of a closed polygon in \(\mathbb{R}^2\).

coordinates¶: (n, 2) numpy.ndarray – Coordinates of vertices of the polygon.

depth¶: int – Depth fractal for each triangle that compose the triangular mesh. If this number is not given, then, the fractal generation of circles is done up to a circle reachs a radius to lower than the five percent of the incircle radius. Large values of depth might produce internal variables that tend to infinte, then a ValueError is produced with a warning message array must not contain infs or NaNs.

Note

The class pckCirclesInPolygon requires NumPy, Matplotlib and Triangle

Examples

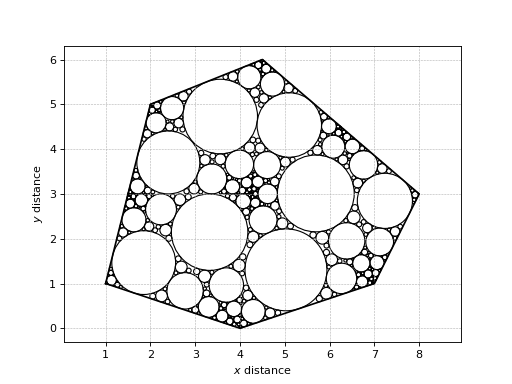
>>> from numpy import array
>>> from circlespacking import pckCirclesInPolygon
>>> coords = array([[1, 1], [2, 5], [4.5, 6], [8, 3], [7, 1], [4, 0]])
>>> pckCircles = pckCirclesInPolygon(coords)
>>> pckCircles.__dict__.keys()
dict_keys(['coordinates', 'depth', 'CDT', 'listCircles'])

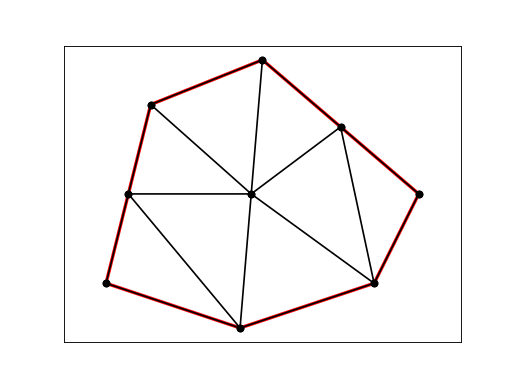
trianglesMesh()[source]¶

Method to generate a triangles mesh in a polygon by using Constrained Delaunay triangulation.

Returns:	Vertices of each triangle that compose the triangular mesh. n means the number of triangles; (3, 2) means the index vertices and the coordinates (x, y) respectively.
Return type:	verts ((n, 3, 2) numpy.ndarray)

Examples

>>> from numpy import array
>>> from basegeometry import Polygon
>>> from circlespacking import pckCirclesInPolygon
>>> coordinates = array([[1, 1], [2, 5], [4.5, 6], [6, 4], [8, 3],
                         [7, 1], [4.5, 1], [4, 0]])
>>> polygon = Polygon(coordinates)
>>> boundCoords = polygon.boundCoords
>>> pckCircles = pckCirclesInPolygon(boundCoords)
>>> verts = pckCircles.trianglesMesh()

>>> from numpy import array
>>> from basegeometry import Polygon
>>> from circlespacking import pckCirclesInPolygon
>>> coordinates = array([[2, 2], [2, 6], [8, 6], [8, 2]])
>>> polygon = Polygon(coordinates)
>>> boundCoords= polygon.boundCoords
>>> pckCircles = pckCirclesInPolygon(boundCoords)
>>> verts =  pckCircles.trianglesMesh()

generator()[source]¶

Method to generate circular particles in each triangle of the triangular mesh.

Returns:	list that contain all the circles object packed in the polygon.
Return type:	listCircles (list of Circle objects)

Examples

>>> from numpy import array
>>> from circlespacking import pckCirclesInPolygon
>>> coords = array([[2, 2], [2, 6], [8, 6], [8, 2]])
>>> pckCircles = pckCirclesInPolygon(coords)
>>> lstCircles = pckCircles.generator() # list of circles

plot(plotTriMesh=False)[source]¶

Method for show a graphic of the circles generated within of the polyhon.

Parameters:	plotTriMesh (bool) – Variable to check if it also want to show the graph of the triangles mesh. The default value is `False`

Examples

(Source code)

(png, hires.png, pdf)

(png, hires.png, pdf)

>>> from numpy import array
>>> from basegeometry import Polygon
>>> from circlespacking import pckCirclesInPolygon
>>> coordinates = array([[1, 1], [2, 5], [4.5, 6], [6, 4], [8, 3],
                         [7, 1], [4.5, 1], [4, 0]])
>>> polygon = Polygon(coordinates)
>>> boundCoords = polygon.boundCoords
>>> pckCircles = pckCirclesInPolygon(boundCoords)
>>> pckCircles.plot()

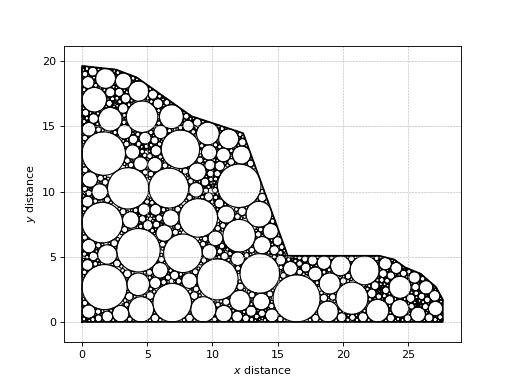
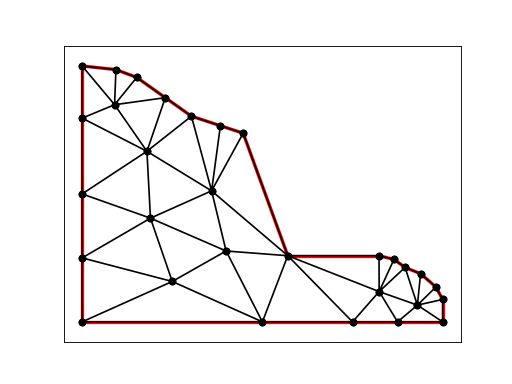
>>> from slopegeometry import AnthropicSlope
>>> from circlespacking import pckCirclesInPolygon
>>> slopeGeometry = AnthropicSlope(12, [1, 1.5], 10, 10)
>>> boundCoords = slopeGeometry.boundCoords
>>> pckCircles = pckCirclesInPolygon(boundCoords)
>>> pckCircles.plot(plotTriMesh=True)