1. basegeometry module

Module to define the Triangle, Circle and Polygon classes. Some properties related to the geometry of these classes are determined. These classes are the basic inputs to pack circular particles in a closed polygon in \(\mathbb{R}^2\).

class basegeometry.Circle(center, radius)

Bases: object

Creates an instance of an object that defines a Circle once the cartesian coordinates of its center and the radius are given.

center

tuple or list – (x, y)-cartesian coordinates of circle center.

radius

float or int – Length of the segment that joins the center with any point of the circumference.

Examples

>>> center, radius = (0, 0), 1
>>> circle = Circle(center, radius)
>>> circle.__dict__
{'area': 3.141592653589793,
 'center': array([0, 0]),
 'curvature': 1.0,
 'diameter': 2,
 'perimeter': 6.283185307179586,
 'radius': 1}

>>> center, radius = (2, 5), 2.5
>>> circle = Circle(center, radius)
>>> circle.__dict__
{'area': 19.634954084936208,
'center': array([2, 5]),
'curvature': 0.4,
'diameter': 5.0,
'perimeter': 15.707963267948966,
'radius': 2.5}

Note

The class Circle requires NumPy

descartesTheorem(circle1, circle2=None)

Method to determine the tangent circles of the Descartes theorem.

To find centers of these circles, it calculates the intersection points of two circles by using the construction of triangles, proposed by Paul Bourke, 1997.

Parameters:

circle1 (circle object): Tangent circle to the circle object intantiated. circle2 (circle object): Tangent circle to the circle object intantiated and to the circle1.

Returns:Each element of the tuple is a circle object. Return type:circles (tuple)

Examples

>>> import matplotlib.pyplot as plt
>>> from basegeometry import Circle
>>> # Special case Descartes' Theorem (cicle with infite radius)
>>> circle = Circle((4.405957, 2.67671461), 0.8692056336001268)
>>> circle1 = Circle((3.22694724, 2.10008003), 0.4432620600509628)
>>> c2, c3 = circle.descartesTheorem(circle1)
>>> # plotting
>>> plt.axes()
>>> plt.gca().add_patch(plt.Circle(circle.center,
                        circle.radius, fill=False))
>>> plt.gca().add_patch(plt.Circle(circle1.center,
                        circle1.radius, fill=False))
>>> plt.gca().add_patch(plt.Circle(c2.center,
                        c2.radius, fc='r'))
>>> plt.gca().add_patch(plt.Circle(c3.center,
                        c3.radius, fc='r'))
>>> plt.axis('equal')
>>> plt.show()

>>> import matplotlib.pyplot as plt
>>> from basegeometry import Circle
>>> # General case Descartes Theorem (three circle tangent mutually)
>>> circle = Circle((4.405957, 2.67671461), 0.8692056336001268)
>>> circle1 = Circle((3.22694724, 2.10008003), 0.4432620600509628)
>>> circle2 = Circle((3.77641134, 1.87408749), 0.1508620255299397)
>>> c3, c4 = circle.descartesTheorem(circle1, circle2)
>>> # plotting
>>> plt.axes()
>>> plt.gca().add_patch(plt.Circle(circle.center,
                        circle.radius, fill=False))
>>> plt.gca().add_patch(plt.Circle(circle1.center,
                        circle1.radius, fill=False))
>>> plt.gca().add_patch(plt.Circle(circle2.center,
                        circle2.radius, fill=False))
>>> plt.gca().add_patch(plt.Circle(c3.center,
                        c3.radius, fc='r'))
>>> plt.axis('equal')
>>> plt.show()

class basegeometry.Triangle(coordinates)

Bases: object

Creates an instance of an object that defines a Triangle once the coordinates of its three vertices in cartesian \(\mathbb{R}^2\) space are given.

It considers the usual notation for the triangle ABC in which A, B and C represent the vertices and a, b, c are the lengths of the segments BC, CA and AB respectively.

coordinates

(3, 2) numpy.ndarray – Coordinates of three vertices of the triangle.

Note

The class Triangle requires NumPy, SciPy and Matplotlib.

Examples

>>> from numpy import array
>>> from basegeometry import Triangle
>>> coords = array([(2, 1.5), (4.5, 4), (6, 2)])
>>> triangle = Triangle(coords)
>>> triangle.__dict__.keys()
dict_keys(['vertices', 'area', 'sides', 'perimeter', 'distToIncenter',
           'incircle'])

>>> from numpy import array
>>> from basegeometry import Triangle
>>> coords = array([[2, 1], [6, 1], [4, 5.5]])
>>> triangle = Triangle(coords)
>>> triangle.__dict__.keys()
dict_keys(['vertices', 'area', 'sides', 'perimeter', 'distToIncenter',
           'incircle'])

getGeomProperties()

Method to set the attributes to the instanced object

The established geometric attributes are the following:

• Area.
• Lenght of its three sides.
• Perimeter.
• Incircle (Circle Object)
• Distance of each vertice to incenter.

packCircles(depth=None, want2plot=False)

Method to pack circular particles within of a triangle. It apply the Descartes theorem (special and general case) to generate mutually tangent circles in a fractal way in the triangle.

Parameters:

• depth (int) – Fractal depth. Number that indicate how many circles are fractally generated from the incirle to each vertice of the triangle. If this number is not given, then, the fractal generation of circles is done up to a circle reachs a radius to lower than the five percent of the incircle radius.
• want2plot (bool) – Variable to check if a plot is wanted. The default value is False.

Returns:

list that contains all the circular particles packed in the triangle.

Return type:

listCircles (list)

Note

Large values of depth might produce internal variables that tend to infinte, then a ValueError is produced with a warning message array must not contain infs or NaNs.

Examples

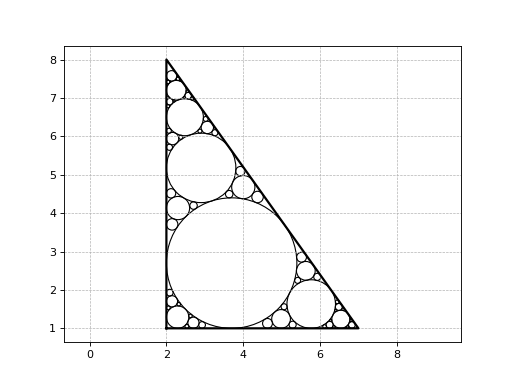
>>> from numpy import array
>>> from basegeometry import Triangle
>>> coords = array([(2, 1.5), (4.5, 4), (6, 2)])
>>> triangle = Triangle(coords)
>>> cirsInTri = triangle.packCircles(depth=2, want2plot=True)

>>> from numpy import array
>>> from basegeometry import Triangle
>>> coords = array([[2, 1], [6, 1], [4, 5.5]])
>>> triangle = Triangle(coords)
>>> cirsInTri = triangle.packCircles(depth=5, want2plot=True)

(Source code, png, hires.png, pdf)

plotTriangle()

Method for show a graphic of the triangle object.

Returns:object associated with a matplotlib graphic. Return type:ax (matplotlib.axes._subplots.AxesSubplot)

Examples

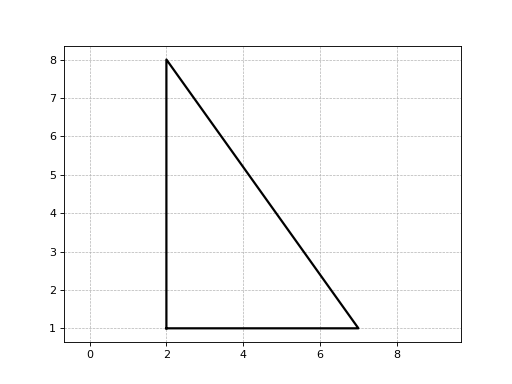
>>> from numpy import array
>>> from basegeometry import Triangle
>>> coords = array([(1, 1), (4, 8), (8, 5)])
>>> triangle = Triangle(coords)
>>> triangle.plotTriangle()

(Source code, png, hires.png, pdf)

class basegeometry.Polygon(coordinates)

Bases: object

Creates an instance of an object that defines a Polygon once the cartesian coordinates of its vertices are given.

coordinates

(n, 2) numpy.ndarray – Coordinates of the vertices of the polygon.

area()

Method for determine the area of the polygon.

Returns:area of the polygon surface. Return type:area (float)

Examples

>>> from numpy import array
>>> from basegeometry import Polygon
>>> coords = array([(1, 1), (4, 8), (8, 5)])
>>> polygon = Polygon(coords)
>>> polygon.area
18.5

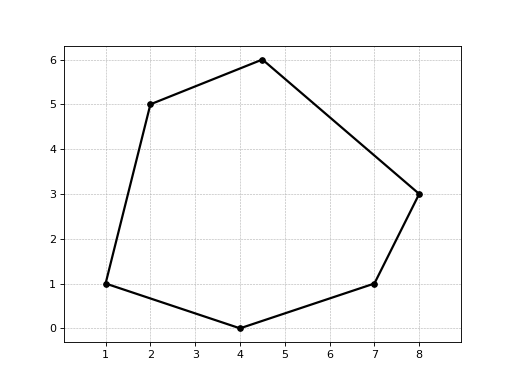
>>> from numpy import array
>>> from basegeometry import Polygon
>>> coords = array([[1, 1], [2, 5], [4.5, 6], [8, 3],
                    [7, 1], [4, 0]])
>>> polygon = Polygon(coords)
>>> polygon.area
27.5

plot()

Method for show the graph of the polygon.

Examples

(Source code, png, hires.png, pdf)